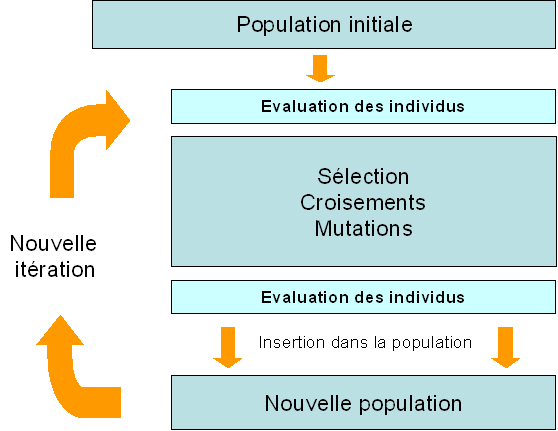
Introduction▲
Parmi tous les types d'algorithmes existants, certains ont la particularité de s'inspirer de l'évolution des espèces dans leur cadre naturel. Ce sont les algorithmes génétiques. Les espèces s'adaptent à leur cadre de vie qui peut évoluer, les individus de chaque espèce se reproduisent, créant ainsi de nouveaux individus, certains subissent des modifications de leur ADN, certains disparaissent…
Un algorithme génétique va reproduire ce modèle d'évolution dans le but de trouver des solutions pour un problème donné. Il sera fait usage dans ce cours de termes empruntés au monde des biologistes et des généticiens et ceci afin de mieux représenter chacun des concepts abordés :
- dans notre cas, une population sera un ensemble d'individus ;
- un individu sera une solution à un problème donné ;
- un gène sera une partie d'une solution, donc d'un individu ;
- une génération est une itération de notre algorithme.
Un algorithme génétique va faire évoluer une population dans le but d'en améliorer les individus. Et c'est donc, à chaque génération, un ensemble d'individus qui sera mis en avant et non un individu particulier. Nous obtiendrons donc un ensemble de solutions pour un problème et pas une solution unique. Les solutions trouvées seront généralement différentes, mais seront d'une qualité équivalente. Nous reviendrons sur cette notion de qualité des solutions dans la partie 2.
Le déroulement d'un algorithme génétique peut être découpé en cinq parties :
- La création de la population initiale ;
- L'évaluation des individus ;
- La création de nouveaux individus ;
- L'insertion des nouveaux individus dans la population ;
- Réitération du processus.
Pour illustrer ce tutoriel, je montrerai comment appliquer un algorithme génétique au problème bien connu de « l'informaticien en vacances », inspiré du problème du voyageur de commerce. L'informaticien en vacances doit visiter plusieurs villes durant ses vacances : { A,B,C,D,E,F,G,H,I,J }. Il cherche donc le chemin le plus court pour passer par chacune d'elles. Il souhaite également assister à un maximum de festivals musicaux (ayant lieu dans les villes A,B et C). Il s'agit donc d'un problème bicritère (la distance entre les villes à minimiser et le nombre de festivals auxquels il pourra assister à maximiser). Chaque festival a lieu à une date donnée. Nous connaissons aussi les distances entre toutes les villes.
I. La création de la population initiale▲
Pour démarrer un algorithme génétique, il faut lui fournir une population à faire évoluer. La manière dont le programmeur va créer chacun des individus de cette population est entièrement libre. Il suffit que tous les individus créés soient de la forme d'une solution potentielle, et il n'est nullement besoin de songer à créer de bons individus. Ils doivent juste rentrer dans le 'moule' du problème posé.
Par exemple, si vous cherchez un chemin entre deux points, les individus créés devront simplement posséder le bon point de départ et le bon point d'arrivée, peu importe par où ils passent. De même si vous cherchez des solutions pour un jeu d'échecs, il suffira que les individus créés possèdent des mouvements autorisés sur des pièces existantes. Même si les individus créés n'ont aucune chance d'être des solutions acceptables pour le problème posé, ils peuvent en avoir la forme. Il n'y a donc aucune objection à les mettre dans la population initiale.
I-A. Et le hasard dans tout ça ?▲
Il est tout à fait possible de créer les individus de manière aléatoire. Et cette méthode amène un concept très utile dans les algorithmes génétiques : la diversité. Plus les individus de la population de départ seront différents les uns des autres, plus nous aurons de chances d'y trouver, non pas la solution parfaite, mais de quoi fabriquer les meilleures solutions possibles.
|
Problème de l'informaticien en vacances |
|---|
|
Nous n'allons pas parcourir tous les chemins possibles, il y en aurait trop. Nous créons une population d'individus au hasard : par exemple {A,B,C,D,E,F,G,H,I,J}, {D,A,F,J,C,E,G,H,B,I}, {J,A,H,F,D,C,I,G,E,B} ou encore {J,F,A,C,B,E,I,H,G,D}. |
I-B. La taille de la population à manipuler▲
La taille de la population initiale est également laissée à l'appréciation du programmeur. Il n'est souvent pas nécessaire d'utiliser des populations démesurées. Une taille de 100 ou 150 individus s'avèrera souvent amplement suffisante, tant pour la qualité des solutions trouvées que pour le temps d'exécution de notre algorithme. Évidemment, ce n'est qu'un ordre de grandeur. Ensuite, libre à vous de modifier la taille de la population initiale en fonction du problème à résoudre si les solutions trouvées ne vous conviennent pas
II. L'évaluation des individus▲
Une fois que la population initiale a été créée, nous allons en sortir les individus les plus prometteurs, ceux qui vont participer à l'amélioration de notre population. Nous allons donc attribuer une 'note' ou un indice de qualité à chacun de nos individus. La méthode d'évaluation des individus est laissée au programmeur en fonction du problème qu'il a à optimiser ou à résoudre.
Cette étape intermédiaire d'évaluation peut même devenir une étape importante du processus d'amélioration de notre population. En effet, les différents individus ne sont pas toujours comparables, il n'est pas toujours possible de dire qu'un individu est meilleur ou moins bon qu'un autre. C'est le cas des problèmes multicritères, lorsqu'une solution dépend de plusieurs paramètres. Vous pourrez toujours dire qu'un nombre est supérieur ou non à un autre, mais vous ne pourrez pas dire si un vecteur est supérieur ou non à un autre. La notion de supériorité pour les vecteurs n'existe pas. Vous pouvez comparer leur norme, mais pas les vecteurs eux-mêmes.
Par exemple si vous souhaitez diminuer un coût de production et un temps de production ; ces deux facteurs ne vont pas forcément de pair et un individu pourra être très bon sur un critère et très mauvais sur un autre. Le recours à l'optimisation d'un problème multicritère empêche de privilégier un critère par rapport à un autre, sans quoi on pourrait tout de suite réécrire le problème pour ne chercher à optimiser que le coût de production sans tenir compte du temps de production. On se ramènerait ainsi à des individus ne dépendant plus que d'un seul critère, ils seraient donc tous comparables. Oui, mais si on ne peut pas privilégier un critère par rapport à un autre, comment comparer deux individus, puisqu'on ne peut pas, à priori, comparer deux vecteurs ?
Libre à vous d'implémenter votre propre méthode d'évaluation des individus. Si vous n'êtes pas inspiré, je vous en présente deux. Il en existe une foultitude d'autres et il ne tient qu'à vous de créer la vôtre, en fonction du problème que vous avez à résoudre.
II-A. Deux méthodes d'évaluation d'individus en contexte multicritère▲
Les méthodes que je vous présente utilisent abondamment la notion de dominance d'individu.
On dit qu'un individu en domine un autre s'il est meilleur dans chacun des critères, pris séparément.
Attention : pour chaque couple d'individus, il n'y en a pas forcément un qui domine l'autre.
|
Problème de l'informaticien en vacances |
|---|
|
L'évaluation du critère relatif à la distance parcourue est simplement la somme de toutes les distances parcourues. |
Méthode 1 : le rang d'un individu est le nombre d'individus qui le dominent + 1. Les meilleurs individus au sens de cette première méthode sont ceux de rang le plus faible. Inconvénient : plusieurs individus peuvent avoir le même rang, tout en étant très différents.
Méthode 2 : le rang d'un individu est l'indice de la population dans laquelle il a été remarqué comme n'étant dominé par aucun autre individu. J'explique. De votre ensemble d'individus, vous sortez ceux qui ne sont dominés par aucun autre individu, et vous leur attribuez le rang 1. Sur les individus qui ne sont pas sortis du lot, vous recommencez l'opération, en cherchant ceux qui ne sont dominés par aucun des individus restants et vous leur attribuez le rang 2 et ainsi de suite jusqu'à épuisement de la population. Les individus jugés les meilleurs sont ceux de rang le plus faible.
Vous trouverez de plus amples informations sur les méthodes d'évaluation en contexte multicritère dans les documentations des algorithmes NDS et NSGA dont sont tirées les méthodes ci-dessus.
L'étape d'évaluation des individus peut être effectuée avant et/ou après les étapes de croisement et de mutations. Une fois encore, le programmeur est libre d'implémenter cette méthode comme bon lui semble.
III. La création de nouveaux individus▲
III-A. La sélection▲
Nous allons maintenant enrichir notre population en croisant des individus. Nous allons essayer de prendre des morceaux de solution de certains individus et d'autres morceaux d'autres individus pour créer des nouveaux individus qui, on l'espère, seront des solutions meilleures à notre problème.
Il est tout à fait possible de choisir des individus au hasard et de les mélanger aléatoirement pour créer de nouveaux individus. Je vais détailler ici quelques-unes des méthodes de sélections souvent utilisées : la roulette, la sélection par rang, la sélection par tournoi et l'élitisme.
III-A-1. La roulette▲
La sélection des individus par le système de la roulette s'inspire des roues de loterie. À chacun des individus de la population est associé un secteur d'une roue. L'angle du secteur étant proportionnel à la qualité de l'individu qu'il représente. Vous tournez la roue et vous obtenez un individu. Les tirages des individus sont ainsi pondérés par leur qualité. Et presque logiquement, les meilleurs individus ont plus de chances d'être croisés et de participer à l'amélioration de notre population.
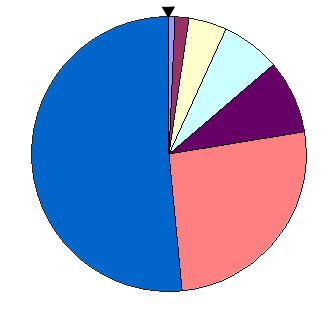
III-A-2. La sélection par rang▲
La sélection par rang est une variante du système de roulette. Il s'agit également d'implémenter une roulette, mais cette fois-ci les secteurs de la roue ne sont plus proportionnels à la qualité des individus, mais à leur rang dans la population triée en fonction de la qualité des individus.
D'une manière plus parlante, il faut trier la population en fonction de la qualité des individus puis leur attribuer à chacun un rang. Les individus de moins bonne qualité obtiennent un rang faible (à partir de 1). Et ainsi en itérant sur chaque individu on finit par attribuer le rang N au meilleur individu (où N est la taille de la population). La suite de la méthode consiste uniquement en l'implémentation d'une roulette basée sur les rangs des individus. L'angle de chaque secteur de la roue sera proportionnel au rang de l'individu qu'il représente.
III-A-3. La sélection par tournoi▲
Le principe de la sélection par tournoi augmente les chances pour les individus de piètre qualité de participer à l'amélioration de la population. Le principe est très rapide à implémenter. Un tournoi consiste en une rencontre entre plusieurs individus pris au hasard dans la population. Le vainqueur du tournoi est l'individu de meilleure qualité. Vous pouvez choisir de ne conserver que le vainqueur comme vous pouvez choisir de conserver les deux meilleurs individus ou les trois meilleurs. À vous de voir, selon que vous souhaitez créer beaucoup de tournois, ou bien créer des tournois avec beaucoup de participants ou bien mettre en avant ceux qui gagnent les tournois haut la main. Vous pouvez faire participer un même individu à plusieurs tournois. Une fois de plus, vous êtes totalement libre quant à la manière d'implémenter cette technique de sélection.
III-A-4. L'élitisme▲
Cette méthode de sélection permet de mettre en avant les meilleurs individus de la population. Ce sont donc les individus les plus prometteurs qui vont participer à l'amélioration de notre population. Cette méthode a l'avantage de permettre une convergence (plus) rapide des solutions, mais au détriment de la diversité des individus. On prend en effet le risque d'écarter des individus de piètre qualité, mais qui aurait pu apporter de quoi créer de très bonnes solutions dans les générations suivantes.
Une autre possibilité relevant aussi du domaine de l'élitisme, pour s'assurer que les meilleurs individus feront effectivement partie de la prochaine génération, est tout simplement de les sauvegarder pour pouvoir les rajouter à coup sûr dans la population suivante (en étape 4).
Le nombre d'individus que vous allez sélectionner en vue d'un croisement ou d'une mutation est encore une fois laissé à votre appréciation. Pensez juste qu'il n'est pas nécessaire (et pas recommandé non plus) de modifier tous les individus d'une population.
Les méthodes de sélection permettent de déterminer quels individus nous allons croiser. Reste maintenant à définir comment nous allons les croiser.
III-B. Les croisements▲
Les croisements permettent de simuler des reproductions d'individus dans le but d'en créer des nouveaux. Il est tout à fait possible de faire des croisements aléatoires. Toutefois, une solution largement utilisée est d'effectuer des croisements multipoints.
III-B-1. Les croisements multipoints▲
Il faut découper en N (2 ou 3 peuvent suffire) morceaux chacun des individus choisis, puis il faut prendre un gène de chaque individu pour créer un nouvel individu.
Notez qu'il est possible de créer ainsi plusieurs individus : si un gène d'un individu ne sert pas à la création d'un individu, il peut servir à la création d'un autre.
Donc en prenant X individus à croiser, vous pouvez potentiellement obtenir X nouveaux individus. Mais rien ne vous empêche d'utiliser plusieurs fois certains gènes, pour obtenir plus de X nouveaux individus.
Notez aussi qu'il n'est pas nécessaire et surtout pas recommandé de croiser tous les individus d'une population, car rien ne nous dit si le résultat d'un croisement sera meilleur ou moins bon que les individus parents.
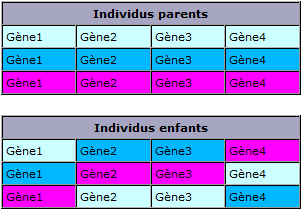
|
Problème de l'informaticien en vacances |
|---|
|
Dans notre exemple, nous ne pouvons pas juste prendre des morceaux des individus parents pour créer les individus enfants. Il faut que les nouveaux individus créés conservent la forme d'une solution potentielle. Ils doivent donc posséder chacune des villes une seule fois. |
III-C. Les mutations▲
Une autre solution que le croisement pour créer de nouveaux individus est de modifier ceux déjà existants. Une fois de plus, le hasard va nous être d'une grande utilité. Il peut s'avérer efficace de modifier aléatoirement quelques individus de notre population en en modifiant un gène ou un autre. Rien ne nous dit que l'individu muté sera meilleur ou moins bon, mais il apportera des possibilités supplémentaires qui pourraient bien être utiles pour la création de bonnes solutions. De même que pour les croisements, il n'est pas recommandé de faire muter tous les individus. Il est possible de faire muter un individu de la manière qu'il vous plaira. Une seule contrainte : l'individu muté doit être de la forme d'une solution potentielle.
Généralement, on ne modifie qu'un gène pour passer d'une solution à une autre solution de forme similaire, mais qui peut avoir une évaluation totalement différente.
|
Problème de l'informaticien en vacances |
|---|
|
La méthode de mutation que je vous propose consiste en une permutation de deux villes. Nous sommes certains que les individus mutés auront toujours la forme d'une solution potentielle, car nous ne changeons que l'ordre des villes. |
IV. L'insertion des nouveaux individus dans la population▲
Une fois que nous avons créé de nouveaux individus que ce soit par croisements ou par mutations, il nous faut sélectionner ceux qui vont continuer à participer à l'amélioration de notre population. Une fois encore, libre au programmeur de choisir ceux qu'il souhaite conserver. Il est possible de refaire une étape d'évaluation des individus nouvellement créés. De même qu'il est possible de conserver tous les nouveaux individus en plus de notre population.
Il n'est toutefois pas recommandé de ne conserver que les nouveaux individus et d'oublier la population de travail. En effet, rien ne nous dit que les nouveaux individus sont meilleurs que les individus de départ.
Une méthode relativement efficace consiste à insérer les nouveaux individus dans la population, à trier cette population selon l'évaluation de ses membres, et à ne conserver que les N meilleurs individus.
IV-A. Comment choisir le nombre N d'individus à conserver ?▲
Le nombre d'individus N à conserver est à choisir avec soin. En prenant un N trop faible, la prochaine itération de l'algorithme se fera avec une population plus petite et elle deviendra de plus en plus petite au fil des générations, elle pourrait même disparaître. En prenant un N de plus en plus grand, nous prenons le risque de voir exploser le temps de traitement puisque la population de chaque génération sera plus grande.
Une méthode efficace est de toujours garder la même taille de population d'une génération à l'autre, ainsi il est possible de dérouler l'algorithme sur un grand nombre de générations.
IV-B. Et on passe à la génération suivante▲
Une fois la nouvelle population obtenue, vous pouvez recommencer le processus d'amélioration des individus pour obtenir une nouvelle population et ainsi de suite …
V. Réitération du processus▲
Le programmeur a l'opportunité d'évaluer les individus de sa population avant et/ou après les phases de création d'individus. En effet, il peut s'avérer pertinent de les évaluer avant de les insérer dans la future population, de même qu'il peut être utile de les réévaluer au début de la génération suivante, si par exemple la méthode d'évaluation dépend de la taille de la population (qui a très bien pu changer). Ainsi on peut être amené à évaluer deux fois par génération chacun des individus.
Le nombre de générations est aussi laissé à l'appréciation du programmeur. Généralement il n'est pas possible de trouver des solutions convenables en moins de 10 générations et au bout de 500 générations, les solutions n'évoluent plus. Mais ceci n'est qu'un ordre de grandeur, tout dépend du problème à résoudre.
Une fois le nombre maximum de générations atteint, vous obtenez une population de solutions. Mais rien ne vous dit que la solution théorique optimale aura été trouvée. Les solutions se rapprochent des bonnes solutions, mais sans plus. Ce n'est pas une méthode exacte.
VI. Conclusion▲
Un algorithme génétique vous donne une grande liberté dans le paramétrage et dans l'implémentation des différents traitements. Libre à vous ensuite de modifier tel ou tel paramètre si les solutions obtenues ne vous conviennent pas.
Les algorithmes génétiques ont l'énorme avantage de pouvoir être appliqués dans un grand nombre de domaines de recherche de solution, lorsqu'il n'est pas nécessaire d'avoir la solution optimale, qui prendrait par exemple trop de temps et de ressources pour être calculée (ou tout simplement si personne n'est capable de la trouver de manière théorique).
Liens▲
Remerciements▲
Merci à Loulou24 pour sa relecture.