Génération de terrain par l'algorithme de Perlin !

Vous voulez créer un jeu, il vous faut un terrain, plusieurs solutions s'offrent à vous de le dessiner à la main une fois pour toutes ou bien le faire générer par votre programme. Si vous choisissez de le dessiner à la main, vous aurez une très grande liberté et un très grand contrôle de votre terrain, il sera exactement comme vous le souhaitez, mais si vous voulez que votre jeu ait dix terrains différents, il vous faudra les créer un par un et les livrer avec votre jeu.

Tandis que si vous choisissez de faire générer vos terrains par votre jeu, il pourra vous en créer autant que vous voulez, ils seront tous différents, et vous ne serez pas obligé de les fournir avec votre jeu, puisqu'ils pourront être régénérés. C'est de cette méthode que je vais parler, en expliquant un algorithme qui fonctionne très bien : l'algorithme de Perlin.

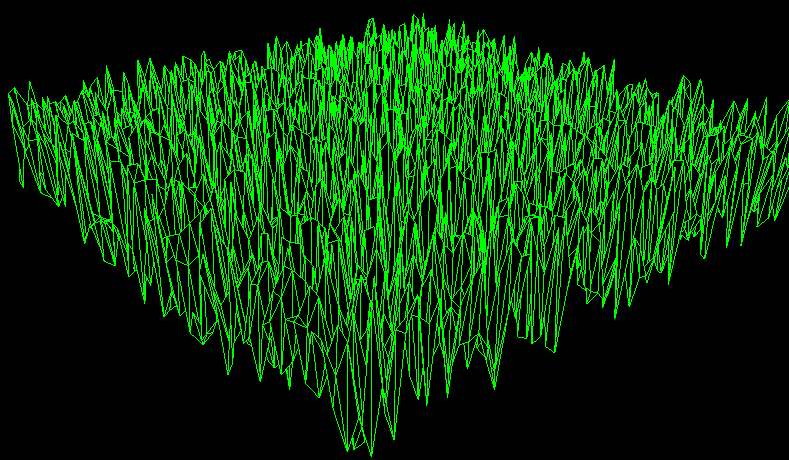
Pour générer un terrain aléatoire, la première idée (naïve) qui vient à l'esprit est de générer une hauteur aléatoire pour chaque position du terrain. Ceci donne des résultats très inexploitables. En effet, le terrain généré n'a aucune cohérence, il ressemble à tout sauf à un terrain.

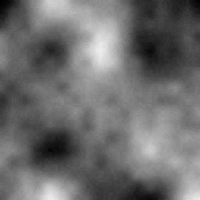
Je vais m'appuyer sur l'article de Fearyourself sur la génération de textures procédurales de terrain et de son viewer de terrain pour visualiser mes résultats. Je vais donc fournir mes résultats sous forme d'une image en niveaux de gris dont la nuance représente la hauteur à chaque position du terrain.

En donnant une valeur entièrement aléatoire à chaque position du terrain, on obtient le résultat suivant :

Si vous n'êtes pas convaincu que ce terrain ne ressemble à rien, je vous invite à le tester dans le viewer de terrain de Fearyourself :

L'idée de l'algorithme de Perlin est d'affiner un terrain par itérations successives tout en interpolant entre les valeurs connues.

Je m'explique : la génération commence en fixant quelques valeurs puis en interpolant tous les autres points à partir de ces valeurs. À ce stade-là, le résultat commence à ressembler à un terrain, mais il n'est pas naturel pour un sou. Il va falloir ensuite lui ajouter des « calques » successifs pour affiner la pente du terrain et lui donner un aspect réaliste.

La structure de données que je choisis est celle d'un « calque ». Un calque va représenter une image en niveau de gris, c'est sur un calque qu'on fera toutes les interpolations. Chaque calque sera aussi muni d'un attribut noté persistance qui définira un niveau sur les données de calque. J'y reviendrai plus tard.

struct calque{
        int **v;
        int taille;
        float persistance;
        };

Les données sont stockées dans le int **. Les données seront des entiers compris entre 0 et 255, image en niveau de gris oblige. J'ai néanmoins choisi le type int pour pouvoir gérer correctement les cas où les valeurs seraient amenées à dépasser 255, pour éviter les dépassements de capacité et les résultats aberrants.

Les terrains générés seront toujours carrés, c'est pourquoi je n'ai besoin que d'un seul attribut taille.

J'ai écrit les fonctions de création et de destruction de calques qui vont bien : elles sont assimilables au constructeur et au destructeur qu'on retrouve en C :

struct calque* init_calque(int t, float p){
  struct calque *s = malloc(sizeof(struct calque));
  s->v = malloc(t*sizeof(int*));
  int i,j;
  for (i=0; i<t ; i++){
    s->v[i]= malloc(t*sizeof(int));
    for (j=0; j<t; j++)
      s->v[i][j]=0;
  }
  s->taille = t;
  s->persistance = p;
 
  return s;
}
 
void free_calque(struct calque* s){
  int j;
  for (j=0; j<s->taille; j++)
    free(s->v[j]);
  free(s->v);
}

L'autre outil dont j'aurai besoin concerne l'enregistrement de mon calque dans une image. Pour des raisons de simplicité et de compatibilité avec le viewer de terrain, je choisis le format BMP. Je laisse l'écriture du fichier BMP à la bibliothèque SDL. Pour cela, il me faut une fonction d'enregistrement :

void enregistrer_bmp(struct calque *c, const char *filename){
  SDL_Surface *s = SDL_CreateRGBSurface(SDL_SWSURFACE,c->taille, c->taille, 32,0, 0, 0, 0);
  if (!s)
    printf("erreur SDL sur SDL_CreateRGBSurface");
 
  int i,j;
  Uint32 u;
  SDL_PixelFormat *fmt = s->format;
  /* on boucle sur chaque pixel */
  for (i=0; i<c->taille; i++)
    for (j=0; j<c->taille; j++){
      u = SDL_MapRGB  (fmt, (char)c->v[i][j], (char)c->v[i][j], (char)c->v[i][j]);
      colorerPixel(s, i, j, u);
    }
 
  SDL_SaveBMP(s, filename);
  SDL_FreeSurface(s);
}

La fonction colorerPixel, comme son nom l'indique se contente de colorer un pixel de l'image. Voici son code :

void colorerPixel(SDL_Surface* s, int x, int y, Uint32 coul){
        *((Uint32*)(s->pixels)   x   y * s->w) = coul;
        }

Et le dernier outil dont j'aurai besoin est le générateur de nombres aléatoires (ou pseudo aléatoires).

/* génère un entier entre 0 et a */
        unsigned char aleatoire(float a){
        return (float)rand() / RAND_MAX * a;
        }

Nous allons commencer par générer un calque entièrement aléatoire, sans aucune cohérence, ce calque nous servira à stocker toutes les valeurs aléatoires.

Nous allons ensuite choisir certains points régulièrement espacés dans le calque pour prendre les valeurs aléatoires associées. Toutes les positions entre ces points choisis seront interpolées (linéairement ou autrement). On voit déjà apparaître l'un des paramètres de l'algorithme : le caractère régulièrement espacé des points choisis.

Ce paramètre est noté la fréquence. Choisir une fréquence de 2 signifie que vous prendrez 9 points sur votre calque aléatoire pour commencer les interpolations. En effet, vous coupez un segment en 2 parties, vous avez donc 3 points (le premier, celui du milieu et le dernier). Et comme nous nous plaçons en deux dimensions, nous avons 3x3 valeurs à prendre. Une fois que tout le calque aura été interpolé entre ces (fréquence 1)² valeurs, nous allons créer un autre calque avec d'autres interpolations, plus fines.

Chaque nouveau calque sera créé exactement de la même manière que le premier, à la différence près que nous prendrons une fréquence située une octave au-dessus de la fréquence associée au calque précédent. Il faut donc connaître la fréquence de chacun des calques et la fréquence de départ. La fréquence d'un calque étant la fréquence du calque précédent x la fréquence de départ.

Ainsi, avec une fréquence de départ de 2, le premier calque aura une fréquence de 2, le second aura 4, le troisième aura 8, puis 16, 32… et ainsi de suite. Nous voyons ici apparaître un autre paramètre de notre algorithme : le nombre de calques à utiliser. Ce paramètre est en fait un nombre d'octaves à utiliser.

Notez qu'il n'est pas nécessaire que toutes les valeurs choisies aléatoirement sur un calque le soient aussi sur le suivant. L'essentiel étant que les calques correspondent à des interpolations de plus en plus fines, même s'ils ne correspondent pas aux mêmes valeurs aléatoires choisies.

Et la partie astucieuse de l'algorithme consiste à additionner tous ces calques de manière pondérée, de sorte que les calques interpolés finement influent moins que ceux interpolés grossièrement. C'est justement cette pondération qui permet de générer des montagnes, des vallées…

On voit apparaître le dernier paramètre de notre algorithme : les pondérations des calques. C'est ce que j'avais appelé persistance dans la définition d'un calque.

Pour avoir un résultat correct, la persistance doit être comprise entre 0 et 1. Une persistance de 0.4 signifie que le premier calque sera pondéré de 40 %, que le suivant sera pondéré de 0.4x0.4 = 16 %, le suivant de 0.4x0.4x0.4 = 6.4 %…

Attention ! Une persistance supérieure à 0.5 amènera des incohérences si vous prenez trop d'octaves. En effet, pour une persistance de 0.9, le premier calque sera pondéré de 90 %, le second de 81´%, et leur somme dépasse 100 %, d'où une valeur supérieure à 255 pour un pixel, d'où aberration. Pour pallier ce problème, j'ai rajouté un traitement final pour ramener les valeurs supérieures à 255 dans un intervalle correct. Mais une persistance supérieure à 0.5 n'amènera pas toujours des incohérences, tout dépend du nombre d'octaves. Bref, il y aura incohérence s'il y a trop d'octaves par rapport à la persistance (quand elle est supérieure à 0.5).

V-A. Création du calque aléatoire▲

struct calque *random;
random = init_calque(taille,1);
 
for (i=0; i<taille; i++)
  for (j=0; j<taille; j++)
    random->v[i][j]=aleatoire(256);

V-B. Remplissage des calques▲

for (n=0; n<octaves; n  ){
  for(i=0; i<taille; i++)
    for(j=0; j<taille; j++) {
      a = valeur_interpolee(i, j, f_courante, random);
      mes_calques[n]->v[i][j]=a;
    }
  f_courante*=frequence;
}

V-C. Interpolations des valeurs▲

Nous devons choisir certaines valeurs sur le calque aléatoire, puis interpoler entre ces valeurs. La fréquence va découper notre calque en plusieurs parties. Tout d'abord, il faut déterminer dans quelle partie le point (i,j) est situé, puis récupérer les valeurs du calque aléatoire aux positions qui délimitent cette partie, puis interpoler entre ces valeurs.

La détermination des bornes entourant le point recherché se fait par division entière en fonction de la taille d'un intervalle.

 

Sélectionnez

int valeur_interpolee(int i, int j, int frequence, struct calque *r){
  /* déterminations des bornes */
  int borne1x, borne1y, borne2x, borne2y, q;
  float pas;
  pas = (float)r->taille/frequence;
 
  q = (float)i/pas;
  borne1x = q*pas;
  borne2x = (q 1)*pas;
 
  if(borne2x >= r->taille)
    borne2x = r->taille-1;
 
  q = (float)j/pas;
  borne1y = q*pas;
  borne2y = (q 1)*pas;
 
  if(borne2y >= r->taille)
    borne2y = r->taille-1;
 
  /* récupérations des valeurs aléatoires aux bornes */
  int b00,b01,b10,b11;
  b00 = r->v[borne1x][borne1y];
  b01 = r->v[borne1x][borne2y];
  b10 = r->v[borne2x][borne1y];
  b11 = r->v[borne2x][borne2y];
 
  int v1  = interpolate(b00, b01, borne2y-borne1y, j-borne1y);
  int v2  = interpolate(b10, b11, borne2y-borne1y, j-borne1y);
  int fin = interpolate(v1, v2, borne2x-borne1x , i-borne1x);
 
  return fin;
}

Une fois les valeurs du calque aléatoire récupérées aux bornes de notre intervalle, nous devons faire une interpolation bilinéaire. C'est pourquoi j'ai écrit trois appels à la fonction d'interpolation.

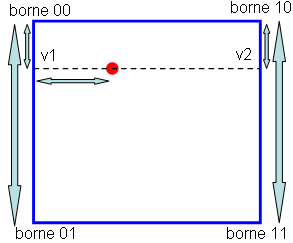
Nous connaissons les valeurs des bornes (elles viennent directement du calque aléatoire), nous interpolons entre ces valeurs pour trouver les valeurs v1 et v2, puis nous interpolons entre v1 et v2 pour avoir la valeur au point recherché.

V-C-1. Choix de l'interpolation▲

Vous pouvez interpoler de la manière que vous voulez, linéairement ou pas. Je vous donne le code pour une interpolation linéaire et pour une non linéaire :

 

Sélectionnez

int interpolate(int y1, int y2, int n, int delta){
            if (n!=0)
            return y1 delta*(y2-y1)/n;
            else
            return y1;
            }

Les valeurs d'entrée étant les valeurs connues entre lesquelles on va interpoler (y1 et y2), l'intervalle entre les valeurs connues (n) et l'intervalle entre la première valeur connue et la valeur recherchée (delta).

Cette interpolation donne des résultats très rapides, très (trop) réguliers, les pentes sont parfaites, elles ne bougent pas d'un poil.

Et voici une interpolation non linéaire :

 

Sélectionnez

int interpolate(int y1, int y2, int n, int delta){
            if (n==0)
            return y1;
            if (n==1)
            return y2;
 
            float a = (float)delta/n;
 
            float v1 = 3*pow(1-a, 2) - 2*pow(1-a,3);
            float v2 = 3*pow(a, 2)   - 2*pow(a, 3);
 
            return y1*v1   y2*v2;
            }

Les valeurs d'entrée sont les mêmes. Voici juste un exemple interpolé avec ces deux méthodes. Les points de base sont marqués en rouge.

On remarque tout de suite que cette interpolation non linéaire nous donne de bien meilleurs résultats, même si elle est un peu plus longue à calculer. Le terrain est beaucoup plus arrondi.

V-D. Ajout de tous les calques▲

Une fois que tous les calques ont été déterminés, il nous reste à les ajouter en tenant compte de la persistance de chacun. C'est à ce moment-là que peuvent surgir les incohérences. Si jamais l'addition finale dépasse 255, nous aurons droit à une aberration. Voici un exemple pour bien vous rendre compte du risque :

Les valeurs supérieures 255 repassent à 0 lorsqu'elles sont enregistrées. C'est la raison pour laquelle il faut surveiller les valeurs obtenues et les corriger si besoin est.

 

Sélectionnez

/* calcul de la somme de toutes les persistances,
pour ramener les valeurs dans un intervalle acceptable */
sum_persistances = 0;
for (i=0; i<octaves; i++)
  sum_persistances =mes_calques[i]->persistance;
 
/* ajout des calques successifs */
for (i=0; i<taille; i++)
  for (j=0; j<taille; j++){
    for (n=0; n<octaves; n++)
      c->v[i][j] =mes_calques[n]->v[i][j]*mes_calques[n]->persistance;
 
    /* normalisation */
    c->v[i][j] =  c->v[i][j] / sum_persistances;
  }

La variable sum_persistances permet d'obtenir une moyenne de tous les calques, pondérés par leur persistance. Ceci garantit des valeurs correctes. Ça a aussi l'avantage et rehausser les niveaux si les persistances sont trop basses. Mais attention, espace discret oblige, en rehaussant des petites valeurs, on perd en précision et on peut obtenir des résultats comme celui-là :

Vous avez une grande liberté dans le paramétrage de cet algorithme, et n'oubliez pas que vous pouvez aussi choisir de faire varier les persistances de manière non géométrique.

Et voilà un terrain réaliste. Si vous le souhaitez, vous pouvez lisser ce terrain :

/* lissage */
struct calque *lissage;
lissage = init_calque(taille, 0);
for (x=0; x<taille; x++)
  for (y=0; y<taille; y++){
    a=0;
    n=0;
    for (k=x-5; k<=x 5; k++)
      for (l=y-5; l<=y 5; l++)
        if ((k >= 0) et (k<taille) et(l>=0) et (l<taille)) {
          n  ;
          a =c->v[k][l];
        }
    lissage->v[x][y] = (float)a/n;
  }

Voici un tableau pour bien voir les actions des paramètres octaves et persistance (sans lissage avec une fréquence de 4) :

• le code source avec le projet Code::Blocks
• Le générateur de textures de fearyourself couplé avec le générateur de terrain

Rappel des commandes.

• La souris permet de faire tourner et zoomer dans le monde.
• La touche 'f' : passer du mode filaire au mode texture.
• La touche 'l' : cycler dans les différents modes d'ombres (l'ordre étant : pas de lumière, avec le simple calcul naïf, avec le simple calcul naïf filtre, le produit scalaire, produit scalaire filtre, le calcul de rayon et le calcul de rayon filtre).
• La touche 'w' : permet de mettre ou enlever l'eau.
• Les flèches droite et gauche : faire une rotation sur un autre angle…
• La touche 'v' pour afficher/masquer le texte.
• La touche 'F2' pour valider les changements de paramètres.
• Les touches 'o' et 'p' pour augmenter ou diminuer la luminosité de la texture.
• Les touches 't' et 'g' pour ajouter ou retirer une octave (pour l'algo de Perlin)
• Les touches 'y' et 'h' pour ajouter ou retirer un dixième de persistance (pour l'algo de Perlin).
• Les touches 'u' et 'j' pour ajouter ou retirer une fréquence (pour l'algo de Perlin).

Je remercie Frank.H pour le coup de pouce en SDL, loka et hansaplast pour leur correction orthographique, et toute l'équipe de la rubrique 2D, 3D, Jeux pour leurs remarques et leur relecture.