I. Qu'est-ce qu'un GAN ?▲
Un réseau GAN est un assemblage de deux réseaux de neurones traditionnels où la fonction de perte de l'un va aider l'apprentissage de l'autre. Le premier réseau est nommé le discriminateur et le second se nomme le générateur.
La fonction de perte d'un réseau est la métrique utilisée pour repérer l'écart entre la sortie réelle du réseau et la sortie attendue. La convergence correspond à une perte nulle.
Un réseau GAN a pour ambition de générer du contenu similaire aux données d'entraînement. Si vous fournissez un ensemble d'images de chats, le réseau GAN pourra générer d'autres images de chats. De nombreuses implémentations ont été popularisées ces dernières années avec notamment la génération automatique de milliers de visages photoréalistes, ou la correction automatique d'images. Cependant les réseaux GAN peuvent être utilisés pour n'importe quel type de données : ils peuvent théoriquement générer de la musique, du texte, des images ou n'importe quel autre type d'information.
Vous pourrez trouver de nombreux projets GitHub implémentant les réseaux GAN dans ces différentes applications.
En cela nous pouvons qualifier les réseaux GAN d'intelligences artificielles, même si ce terme est utilisé dans trop de contextes différents et repose surtout sur des effets d'annonces.
Dans la suite de l'article, je me base sur un réseau GAN dédié à la génération d'images.
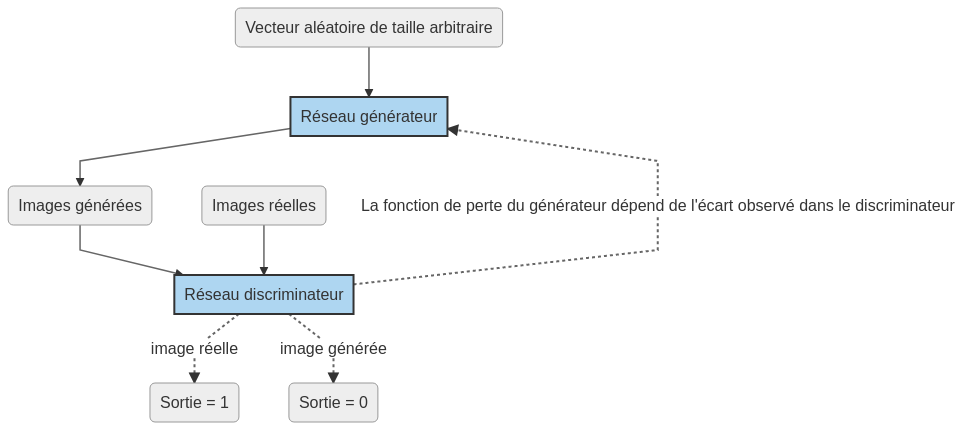
Voici le schéma global d'un réseau GAN.
I-A. Le discriminateur▲
Ce réseau a pour but de déterminer si une image correspond ou non à l'ensemble d'entraînement. Il prend une image en entrée et il a une sortie binaire. L'entraînement est supervisé : une image d'entraînement doit donner une sortie égale à 1 et une image provenant du générateur doit donner une sortie égale à 0.
I-B. Le générateur▲
Ce réseau prend en entrée un vecteur aléatoire et doit générer en sortie une image. Au fur et à mesure que le réseau va apprendre, les images en sortie seront de meilleure qualité.
Les images générées sont soumises au discriminateur qui va les juger et essayer de deviner si elles sont réelles ou pas. L'entraînement du générateur est supervisé : les poids doivent être modifiés pour faire correspondre le vecteur aléatoire en entrée à une perte minimale en sortie du discriminateur.
Les prédictions faites sur un même vecteur aléatoire en entrée du générateur vont s'affiner au fil des générations à la manière d'une image dont la qualité s'améliore avec le temps.
I-C. Entraînements conjoints des deux réseaux▲
Les deux réseaux sont entraînés simultanément, la sortie de l'un alimente le jugement de l'autre. On ne peut pas utiliser la méthode Model.fit de TensorFlow puisque la fonction de perte est spécifique et recalculée à chaque itération.
II. Implémentation▲
Je me base sur l'implémentation proposée sur le site officiel de TensorFlow. L'implémentation génère des images 28x28, inspirées des images des nombres MNIST. En effet, ce jeu de données contient 60 000 images de nombres. Nous allons donc essayer de générer des nouvelles images de nombres, inspirées des images réelles.
Vous pouvez remarquer que j'utilise le terme “inspirer” puisque c'est bien ce comportement “intelligent” que nous allons obtenir ici.
II-A. Le discriminateur▲
C'est un réseau convolutif traditionnel. L'implémentation proposée contient deux couches de convolution et un peu de dropout pour éviter le surapprentissage. On remarque le input_shape=[28,28,1] qui représente une image 28x28 sur un seul canal : c'est l'entrée du réseau. La dernière couche Dense (1) contient juste un neurone, entièrement connecté à la couche précédente.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
def make_discriminator_model():
return tf.keras.Sequential([
tf.keras.layers.Conv2D(64, (5, 5), strides=(2, 2), padding='same', input_shape=[28, 28, 1]),
tf.keras.layers.LeakyReLU(),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Conv2D(128, (5, 5), strides=(2, 2), padding='same'),
tf.keras.layers.LeakyReLU(),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(1)
])
La fonction de perte du discriminateur cumule l'écart entre une prédiction d'image réelle et une prédiction idéale (1) ainsi qu'entre une prédiction d'image générée et une prédiction idéale (0). Le calcul est fait sur un ensemble de sorties, nous manipulons des tableaux de 0 ou de 1, pas uniquement des valeurs scalaires.
2.
3.
4.
def discriminator_loss(real_output, fake_output):
real_entropy = cross_entropy(tf.ones_like(real_output), real_output)
fake_entropy = cross_entropy(tf.zeros_like(fake_output), fake_output)
return real_entropy + fake_entropy
II-B. Le générateur▲
C'est lui aussi un réseau traditionnel. On remarque l'entrée du réseau : input_shape(100,), elle correspond à la taille de notre vecteur aléatoire. L'implémentation propose l'utilisation de couches de déconvolution (Conv2DTranspose) permettant de créer des pixels liés géographiquement. La déconvolution sur une couche 7x7 donne 14x14 pixels puis 28x28, ce qui correspond à sortie de notre réseau.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
def make_generator_model():
return tf.keras.Sequential([
tf.keras.layers.Dense(7*7*256, use_bias=False, input_shape=(100,)),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.LeakyReLU(),
tf.keras.layers.Reshape((7, 7, 256)),
tf.keras.layers.Conv2DTranspose(128, (5, 5), strides=(1, 1), padding='same', use_bias=False),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.LeakyReLU(),
tf.keras.layers.Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', use_bias=False),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.LeakyReLU(),
tf.keras.layers.Conv2DTranspose(1, (5, 5), strides=(2, 2), padding='same', use_bias=False, activation='tanh')
])
La fonction de perte du générateur est plus simple que celle du discriminateur :
def generator_loss(fake_output):
return cross_entropy(tf.ones_like(fake_output), fake_output)C'est ici qu'est fait le bouclage entre le discriminateur et le générateur. On souhaite guider le générateur vers l'idéal 1, on calcule donc l'écart entre les sorties du discriminateur et un résultat idéal : 1. Et c'est cette fonction de perte qui va guider l'apprentissage du générateur.
On peut remarquer que la fonction de perte du générateur cherche à améliorer les générations des images, elle cherche à les rapprocher des images idéales. Tandis que la fonction de perte du discriminateur cherche à considérer les générations comme continuellement fausses. D'une part cela permet au discriminateur d'être plus efficace, mais d'autre part cela permet de constamment demander une meilleure qualité des images générées. Plus vous ferez de générations, plus les résultats seront semblables aux images réelles.
II-C. Déroulement de l'apprentissage▲
L'apprentissage est une boucle qui va acquérir un lot d'images réelles à partir d'un ensemble connu et un lot d'images générées par le générateur. Ces deux lots sont proposés au discriminateur de manière supervisée. Les écarts entre les valeurs attendues sont calculés et sont soumis aux deux réseaux pour qu'ils puissent chacun s'entraîner.
Il y a de nombreux paramètres que vous pouvez modifier :
- le nombre d'images acquises à chaque génération ;
- le nombre de générations ;
- la taille du vecteur aléatoire en entrée du générateur ;
- les fonctions de perte peuvent être encore personnalisées ;
- l'enchaînement des couches de chacun des deux réseaux ;
- l'ajout de dropout ;
- …
Pseudocode
2.
3.
4.
5.
6.
7.
À chaque génération
Collecte de n images réelles
Collecte de n images générées
On soumet les n images réelles pour obtenir les n sorties réelles
On soumet les n images générées pour obtenir les n sorties fausses
On calcule les deux fonctions de perte à partir des écarts des sorties
On adapte les poids des réseaux en fonction des pertes calculées
Régulièrement dans la boucle, vous pouvez repérer ce que devient le vecteur aléatoire d'entrée : ce sont les images générées.
L'exécution de l'entraînement prend beaucoup de temps et vous avez intérêt à avoir du matériel supportant CUDA. Voici une animation GIF représentant l'évolution des générations basées sur un même vecteur aléatoire.
Retrouvez le code complet sur mon dépôt Github.
On remarque qu'au début les images sont aléatoires, rapidement elles ont du contenu centré (grâce aux déconvolutions) et au fur et à mesure de l'apprentissage les formes se précisent et ressemblent de plus en plus à des nombres tels que présents dans le jeu de données MNIST. Nous n'avons ici que des images 28x28x1, je vous laisse imaginer le temps d'apprentissage nécessaire pour générer des images photoréalistes bien plus grandes sur 3 canaux.
Vous aurez besoin de matériel spécifique pour vous lancer dans de telles exécutions, pensez à utiliser le cloud. Plusieurs fournisseurs de cloud public proposent des instances virtuelles dédiées au calcul intensif avec les GPU les plus puissants du moment :
- Google Cloud : https://cloud.google.com/gpu?hl=fr
- IBM Cloud : https://www.ibm.com/fr-fr/cloud/gpu
- Amazon EC2 : https://aws.amazon.com/fr/ec2/instance-types/p2/
- Microsoft Azure : https://docs.microsoft.com/en-us/azure/virtual-machines/sizes-gpu
- OVH : https://www.ovhcloud.com/fr/public-cloud/gpu/
III. Pour aller plus loin▲
Les réseaux GAN sont à l'origine de beaucoup d'innovations récentes. C'est un domaine de recherche très actif et chaque année apporte son lot de nouveautés. L'utilisation de deux réseaux montre qu'il faut voir plus loin que le simple enchaînement de couches d'un même réseau. De nombreuses implémentations restent à imaginer et il existe déjà plusieurs types de réseaux GAN, expérimentés par tel ou tel organisme de recherche. Je vous invite à jouer avec ces réseaux et à apprécier les contenus générés par une telle IA.