Déroulement de l'algorithme▲
L'idée principale est de transposer le problème du monde des graphes au monde des matrices, dont on pourra utiliser les propriétés algébriques pour simplifier le problème.
Le jeu de données est considéré sous la forme d'une matrice d'autant plus remplie que le graphe est “emmêlé”. Une matrice creuse signifiera que le graphe est faiblement connecté, que chaque point n'est relié qu'à ses points immédiatement proches.
Le cas idéal est celui où chaque point n'est relié qu'à deux voisins, formant ainsi un graphe linéaire. La matrice d'un tel graphe sera quasi diagonale. Un tel graphe sera aisé à découper puisqu'il sera en une seule dimension.
L'idée de l'algorithme est de trouver une base propre dans laquelle la matrice de départ s'exprimera sous une forme diagonale, où il sera aisé de repérer des groupes de points en une seule dimension.
Connectivité du dataset▲
Tout d'abord nous devons transformer notre dataset en graphe connecté. Pour cela nous pouvons repérer les points les plus proches de chaque point du dataset et générer un graphe non orienté à partir de ces voisinages.
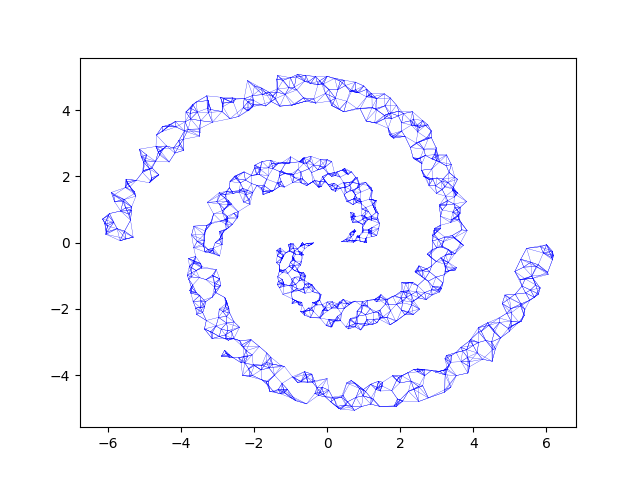
Considérons le dataset suivant :
Remarquons que ce dataset possède deux clusters. Ils ne sont pas convexes et ne sont pas séparables linéairement. Le partitionnement par l'algorithme des k-means s'avérerait inefficace.
En repérant les cinq plus proches voisins, nous pouvons obtenir le graphe suivant :
Le paramètre de connectivité k à choisir dépend de votre ensemble de données. Veillez à ne pas le prendre trop grand.
Matrices de travail▲
Définissons une matrice d'adjacence A indiquant si deux points i et j sont liés par un arc. A(i,j) est égal à 1 si et seulement si les points i et j sont liés dans le graphe.
Définissons une matrice des degrés D, diagonale, indiquant le nombre d'arcs partant de chaque point. En ayant recherché k plus proches voisins, cette matrice doit correspondre à kitxmlcodeinlinelatexdvpD = k * Identite_kfinkitxmlcodeinlinelatexdvp. Dans un cas plus général, la diagonale n'est pas nécessairement composée que de kitxmlcodeinlinelatexdvpkfinkitxmlcodeinlinelatexdvp. Un graphe orienté ou construit différemment contiendra d'autres valeurs diagonales.
Définissons ensuite la matrice laplacienne kitxmlcodeinlinelatexdvpL = D - Afinkitxmlcodeinlinelatexdvp. La matrice laplacienne est au cœur de la théorie spectrale des graphes.
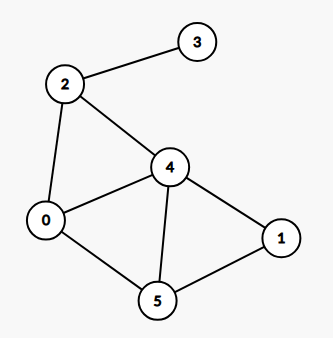
Voici un exemple de matrice laplacienne associée à un graphe simple à six nœuds :
kitxmlcodelatexdvpL = \begin{pmatrix} 3 & 0 & -1 & 0 & -1 & -1 \\ 0 & 2 & 0 & 0 & -1 & -1 \\ -1 & 0 & 3 & -1 & -1 & 0 \\ 0 & 0 & -1 & 1 & 0 & 0 \\ -1 & -1 & -1 & 0 & 4 & -1 \\ -1 & -1 & 0 & 0 & -1 & 3 \end{pmatrix}finkitxmlcodelatexdvpOn remarque que la matrice laplacienne est carrée et symétrique. Les coefficients -1 indiquent une connexion entre les points i et j. La diagonale contient le nombre de connexions par ligne.
Cette matrice est diagonalisable, il existe donc un espace dans lequel elle s'exprime facilement (théorème spectral).
Voici un exemple de code pour générer la matrice laplacienne :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
def genererMatriceLaplacienne(dataset):
nbPointsDuDataset = len(dataset)
matriceLaplacienne = [];
for i in range(nbPointsDuDataset):
ligneLaplacienne = np.zeros(nbPointsDuDataset)
prochesVoisins = trouverLesKPlusProchesVoisins(dataset, i)
# la valeur diagonale est le nombre de connexions au point i
ligneLaplacienne[i] = len(prochesVoisins)
# chaque point connecté est noté -1
for j in prochesVoisins:
ligneLaplacienne[j] = -1
matriceLaplacienne.append(ligneLaplacienne)
return matriceLaplacienne
Valeurs propres▲
La diagonalisation de la matrice L nécessite de rechercher les valeurs propres (eigenvalues) ainsi que les vecteurs propres (eigenvectors). Les valeurs propres représentent le spectre de L. Heureusement numpy est là pour ça :
from numpy import linalg as la
lambdas, xlambdas = la.eig(matriceLaplacienne)xlambdas est une matrice de dimensions n*n, contenant les n vecteurs propres kitxmlcodeinlinelatexdvpX_ifinkitxmlcodeinlinelatexdvp de L. Attention, le i-ième vecteur propre s'obtient en faisant xlambdas[:,i], c'est-a-dire la i-ième colonne de la matrice.
lambdas est le tableau des valeurs propres kitxmlcodeinlinelatexdvp\lambda_ifinkitxmlcodeinlinelatexdvp.
Nous devons trier nos valeurs propres kitxmlcodeinlinelatexdvp\lambda_ifinkitxmlcodeinlinelatexdvp et reporter l'ordre de tri sur les vecteurs propres kitxmlcodeinlinelatexdvpX_ifinkitxmlcodeinlinelatexdvp.
2.
3.
4.
5.
6.
indicesLambdasTries = np.argsort(lambdas)
lambdasTries = lambdas [indicesLambdasTries]
# les vecteurs sont organisés en colonnes et non pas en lignes, il faut faire une double transposition pour les trier
xlambdas = np.transpose(xlambdas)
xlambdasTries = xlambdas[indicesLambdasTries]
xlambdasTries = np.transpose(xlambdasTries)
Après le tri des valeurs propres et des vecteurs propres associés, on peut passer à la suite.
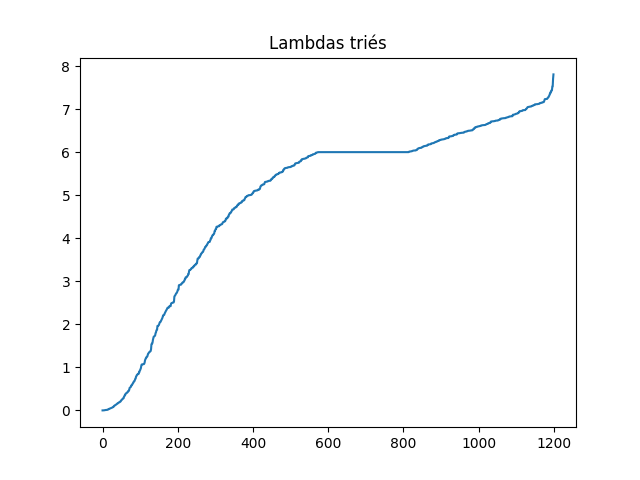
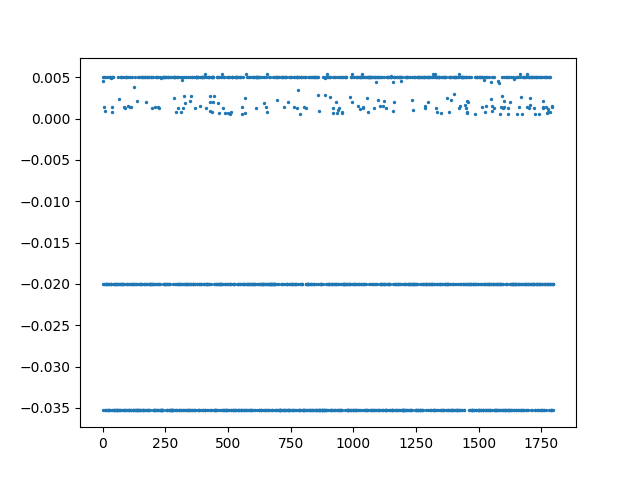
Voici mes valeurs propres triées :
L est une matrice symétrique et semi-définie positive. Elle a, de fait, sa première valeur propre kitxmlcodeinlinelatexdvp\lambda_0finkitxmlcodeinlinelatexdvp qui est toujours nulle. De plus, ses valeurs propres sont réelles. La plus petite valeur propre non nulle suivante donnera l'indice du vecteur propre à étudier par la suite : c'est le vecteur de Fiedler kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp. Il y a un point qui peut être délicat ici, c'est que les premières valeurs propres peuvent être très proches de 0, il est donc nécessaire d'ignorer les premières en les considérant comme nulles. Le seuil kitxmlcodeinlinelatexdvp\epsilonfinkitxmlcodeinlinelatexdvp pour les considérer comme nulles est laissé à votre appréciation. Un autre moyen pour repérer kitxmlcodeinlinelatexdvp\lambda_Ffinkitxmlcodeinlinelatexdvp est de chercher le premier vecteur kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp non constant.
La première valeur propre non nulle kitxmlcodeinlinelatexdvp\lambda_Ffinkitxmlcodeinlinelatexdvp vous donne ensuite le vecteur propre kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp dont la séparation des composantes est aisée puisqu'il est en une dimension.
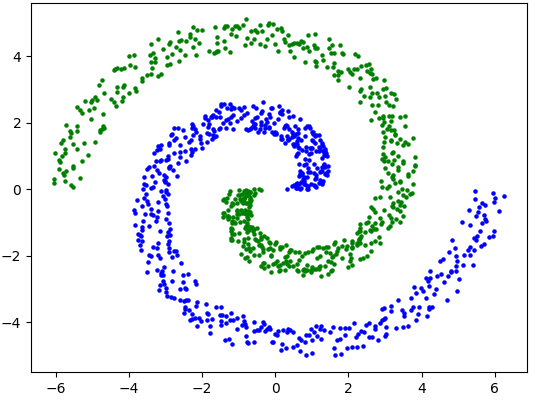
Vous avez plusieurs possibilités pour séparer les composantes de kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp. Vous pouvez fixer un seuil séparant deux clusters comme la moyenne arithmétique. Si la composante i de kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp est associée à un cluster kitxmlcodeinlinelatexdvpCfinkitxmlcodeinlinelatexdvp dans l'espace spectral, alors la donnée i du dataset sera associée au même cluster kitxmlcodeinlinelatexdvpCfinkitxmlcodeinlinelatexdvp dans l'espace de votre dataset.
Nous obtenons ainsi le partitionnement suivant :
Si vous recherchez plus de deux clusters vous pouvez utiliser un k-means pour séparer les composantes de kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp et affecter chaque donnée i en fonction de l'affectation de la composante i de kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp.
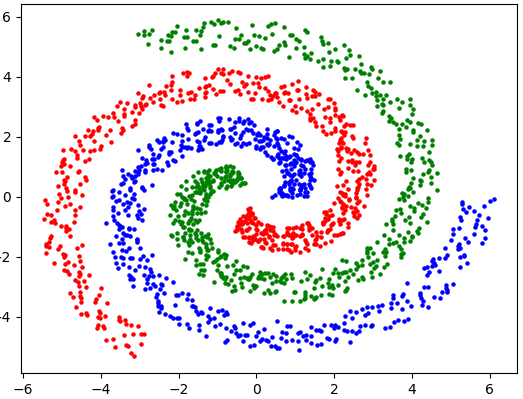
Voici la représentation de kitxmlcodeinlinelatexdvpX_Ffinkitxmlcodeinlinelatexdvp dans le cas d'un dataset contenant trois clusters :
En réalisant une séparation linéaire en trois clusters, nous obtenons le partitionnement suivant :
En conclusion▲
Cette méthode fait appel à des notions plus complexes que les algorithmes de partitionnement k-means et DBSCAN. Elle est plus abstraite et elle demande une compréhension plus fine de l'algèbre linéaire. Même si numpy fait les calculs à votre place, il est nécessaire de comprendre chaque étape.
Cet algorithme n'est pas itératif, il donne d'un coup la solution optimale.
Cette méthode a l'avantage de savoir partitionner des clusters non convexes et de formes quelconques. Mais elle reste sensible au bruit puisqu'elle n'est pas capable de séparer les points extrêmes (contrairement à DBSCAN). La présence de beaucoup de points bruités pourra induire le graphe de connectivité en erreur et compromettre la suite de l'algorithme. Si vous avez un gros dataset, le calcul du partitionnement peut également prendre beaucoup de temps.
Retrouvez le code source ici.
Et bien sûr, comme pour les autres algorithmes présentés précédemment, ne vous embêtez pas à réécrire cet algorithme, il est ici.