Partitionnement hiérarchique de données

Le partitionnement hiérarchique peut être descendant ou ascendant.
On dira qu'il est ascendant quand l'algorithme essaie de fusionner deux clusters en un seul.
On dira qu'il est descendant quand l'algorithme essaie de découper un gros cluster en deux clusters plus petits.
Je vais présenter la méthode ascendante, partant de clusters contenant un seul point et allant jusqu'à l'union de tout le dataset dans un même cluster.

Au démarrage de l'algorithme, il y a autant de clusters que de points, chaque cluster contient un seul point. Itérativement, l'algorithme va chercher quels clusters sont les plus proches pour les fusionner. La notion de « distance entre deux clusters » est centrale dans cet algorithme.

Le pseudocode est assez simple :

création de tous les clusters, contenant chacun un point
tant qu'il y a plusieurs clusters
    trouver les deux clusters les plus proches
    fusionner ces deux clusters

La recherche des clusters les plus proches se formalise par l'utilisation d'une matrice de distances entre clusters, une matrice de dissimilarités kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp.
kitxmlcodeinlinelatexdvpM(i,j)finkitxmlcodeinlinelatexdvp = distance entre les clusters i et j

Cette matrice est symétrique de diagonale nulle. Cette matrice kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp doit se calculer entièrement au début de l'algorithme. Chaque fusion de deux clusters A et B dans le cluster A va mettre à jour la matrice M de la manière suivante :

• suppression de la ligne B et de la colonne B (kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp reste symétrique et de diagonale nulle) ;
• recalcul des distances entre tous les clusters et le cluster A : recalcul de la ligne A (et par symétrie la colonne A).

Voici une partie python illustrant ce partitionnement :

dataset = genererDataset()
clusters = []
# le cluster 0 contient le point 0 ...
for i in range(len(dataset)):
    clusters.append([i])

matriceDissimilarite = genererMatriceDissimilarite(dataset, clusters)
pasTermine = True
while pasTermine:
    # on cherche la similarité la plus proche et non nulle
    cluster1,cluster2,minimum = trouverPlusPetiteDistance(matriceDissimilarite)

    # on doit s'arranger pour que cluster1 soit inférieur à cluster2 
    # sinon on a un souci avec les lignes de la matrice de dissimilarités
          
    # on regroupe cluster1 et cluster2 dans le cluster1
    clusters[cluster1] = np.concatenate( (clusters[cluster1] ,  clusters[cluster2]) )

    # on supprime le cluster 2
    clusters.pop(cluster2)

    # on supprime le cluster2 dans la matrice de matriceDissimilarite en ligne et en colonne
    matriceDissimilarite.pop(cluster2)
    for i in range(len(matriceDissimilarite)):
        matriceDissimilarite[i].pop(cluster2)
    
    # on recalcule la dissimilarité avec cluster1
    for i in range(len(matriceDissimilarite)):
        if i != cluster1:
            matriceDissimilarite[i][cluster1] = matriceDissimilarite[cluster1][i] = calculerDissimilarite(dataset, clusters[i], clusters[cluster1])
     
     # évaluation de la fin de l'algorithme
     pasTermine = stopOuEncore(clusters, minimum)

L'algorithme regroupe les clusters par proximité. Dès lors que les deux clusters A et B à rapprocher sont trop éloignés (kitxmlcodeinlinelatexdvpd(A,B) > \deltafinkitxmlcodeinlinelatexdvp), on peut considérer qu'il n'y a plus de fusions à effectuer.
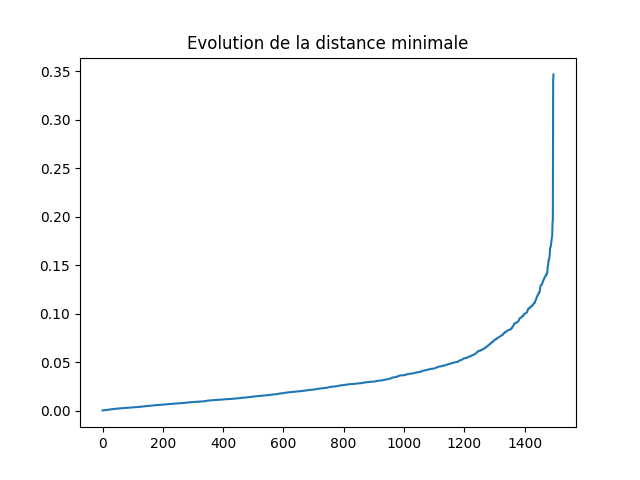
À chaque itération, la distance minimale entre les clusters augmente (sauf pour le cluster qui vient de fusionner, pour lequel il faut attendre une itération). Il est ainsi possible de tracer la courbe de distance minimale et de repérer quand elle change de courbure.

Vous pouvez aussi simplement arrêter l'algorithme une fois que vous avez trouvé les n clusters que vous cherchiez.

Gestion du bruit▲

Plusieurs méthodes sont utilisées pour déterminer la distance entre deux clusters A et B :

• plus grande distance : kitxmlcodeinlinelatexdvpmax_{i,j}( distance(A_i, B_j))finkitxmlcodeinlinelatexdvp
• plus petite distance : kitxmlcodeinlinelatexdvpmin_{i,j}(distance(A_i, B_j))finkitxmlcodeinlinelatexdvp
• distance moyenne : kitxmlcodeinlinelatexdvpmoyenne_{i,j}(distance(A_i, B_j))finkitxmlcodeinlinelatexdvp
• distance de Ward : distance entre les centres de A et de B. On peut calculer ces centres comme les barycentres géométriques des clusters ou en considérant le point le plus proche du barycentre.

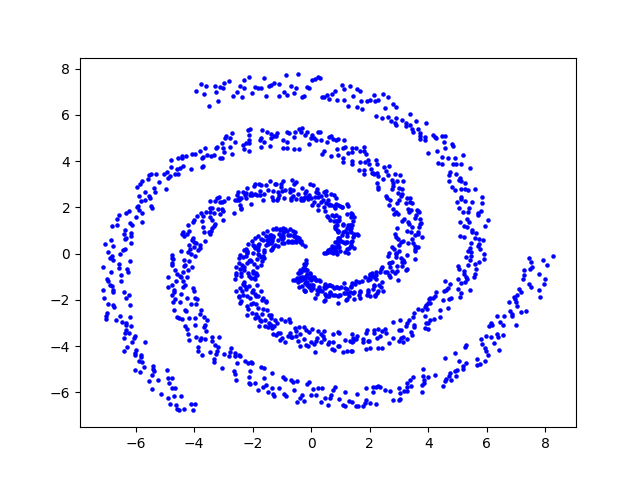
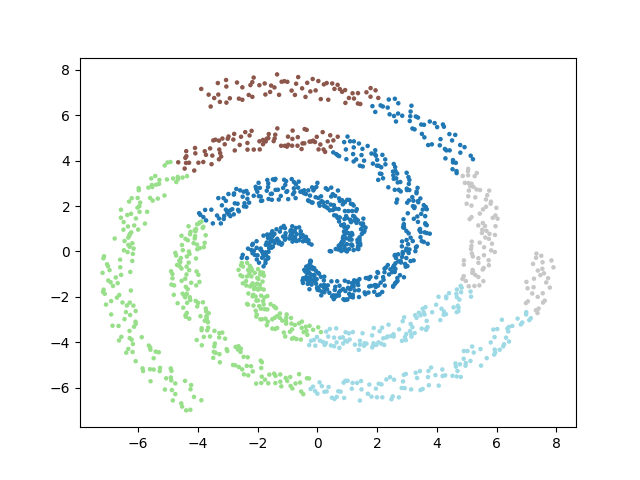
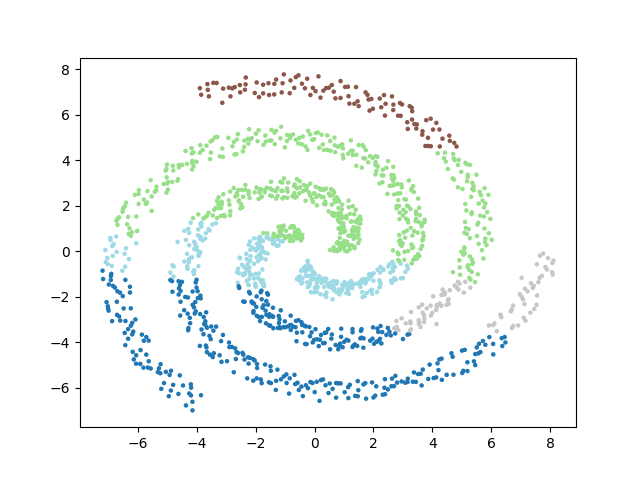
Le choix de la méthode de calcul influe sur la forme des clusters mis en évidence. Comme dans mes articles précédents, je me base sur un dataset contenant trois clusters, disposés en spirales :

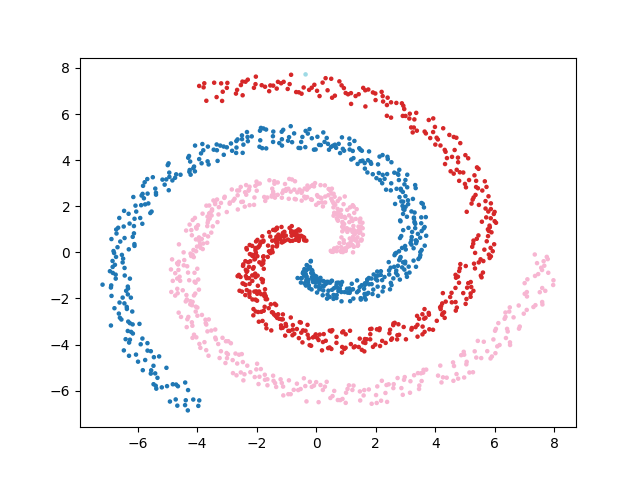
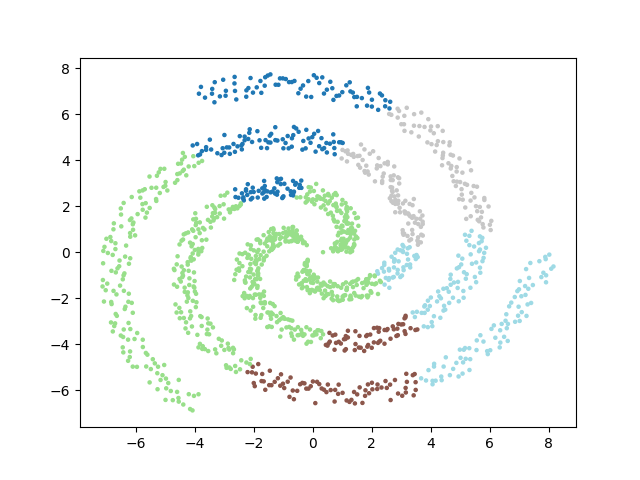
Voici les partitionnements proposés selon les méthodes :

Cet algorithme a la capacité de repérer des clusters de formes quelconques. On peut isoler le bruit assez facilement. Par contre, rien ne garantit que les clusters isolés sont de taille similaire. Sa complexité est très lourde, il y a d'innombrables parcours du dataset pour calculer les distances entre les points des clusters. Même en utilisant des structures spatiales comme les quad-trees, il y aura beaucoup de boucles à réaliser.
Bien souvent on préfèrera des algorithmes plus rapides et moins gourmands.

Vous pouvez retrouver mon implémentation didactique ici. Comme pour les autres méthodes présentées, l'algorithme optimisé est ici.